ReproNim Statistics Module

The positive Predictive Value

Overview

Teaching: 20 min
Exercises: 40 min

Questions

What is the positive Predictive Value (PPV) ?

Objectives

After this lesson, you should understand what is the PPV

Definitions: remiders

$H_0$ : null hypothesis: The hypothesis that the effect we are testing for is null
$H_A$ : alternative hypothesis : Not $H_0$, so there is some signal
$T$ : The random variable that takes value “significant” or “not significant”
$T_S$ : Value of T when test is significant (eg $T = T_S$)
$T_N$ : Value of T when test is not significant (eg $T = T_N$)
$\alpha$ : false positive rate - probability to reject $H_0$ when $H_0$ is true ($H_A$ is false) $= P(T_S \mid H_0)$
$\beta$ : false negative rate - probability to accept $H_0$ when $H_A$ is true ($H_0$ is false) $= P(T_N \mid H_A)$
power = $W = 1-\beta$

PPV : definition

PPV = $P(H_A \mid T_S)$

PPV : How do I compute it ? where does it come from ?

Let’s do some basic probability

We consider that the hypotheses H_0 and H_A are random, i.e. they have associated probabilities. For instance, the probability of $H_0$ to be true could be 20%. We have either $H_A$ is true, or else $H_0$ is true. Therefore:

$P(H_A = True) + P(H_0 = True) = 1$.

We simply note

$P(H_A = True)$ as $P(H_A)$

and

$P(T = T_S)$ as $P(T_S)$

We are interested in the probability of a significant test, we can write

\[P(T_S) = P(T_S, H_A) + P(T_S, H_0)\]

because $T_S$ occurs either under the null or the alternative (mutually exclusive) and their represent all the possibilities.

Bayes theorem

The famous Bayes theorem states:

\[P(A, B) = P(A \mid B) P(B)\]

and therefore

\[P(A \mid B) = \frac{P(A, B)}{P(B)} = \frac{P(B \mid A) P(A)}{P(B)}\]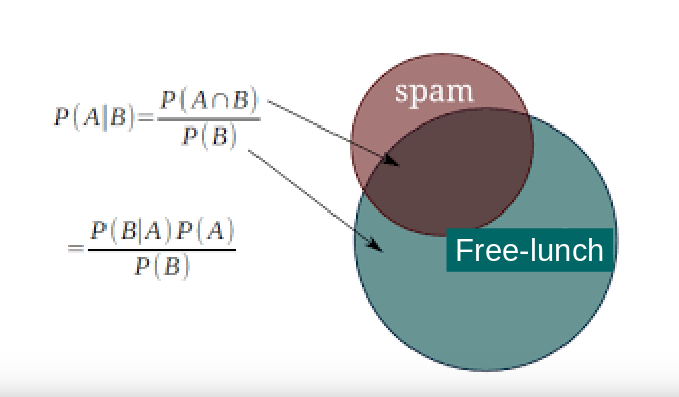

Bayes theorem in image

Apply this to our question:

Now, apply this to the probability of the test results $T$.

The probability of a significant result of the test $T=T_S$ is :

\[P(T_S) = P(T_S, H_A) + P(T_S, H_0)\] \[P(T_S) = P(T_S \mid H_A) P(H_A) + P(T_S \mid H_0) P(H_0)\]

What is the probability of $H_A$ given that the test is significant (eg, PPV) ?

\[P(H_A \mid T_S) = \frac{P(T_S \mid H_A) P(H_A)}{P(T_S)} = \frac{P(T_S \mid H_A) P(H_A)}{P(T_S \mid H_A) Pr(H_A) + Pr(T_S \mid H_0) Pr(H_0)}\]

And we know that

\[P(T_S \mid H_A) = 1 - P(T_N \mid H_A) = 1 - \beta = W\]

Substituting:

\[P(H_A \mid T_S) = \frac{W P(H_A)}{W P(H_A) + \alpha P(H_0)}\]

Defining: $R = \frac{P(H_A)}{P(H_0)}$ the odd ratio of the alternative over the null

\[P(H_A \mid T_S) = \frac{W R}{W R + \alpha}\]

PPV :Some exercises

Task: Play with the PPV - understand the impact of the parameters

Pick a recent study that you have done in fMRI or using anatomical data.  
try to propose values for power, alpha, and prior
Vary power from .1 to .9 and print or plot results

First define a function to compute the PPV from power, odd ratio and alpha
The solution below is in Python, but feel free to do it in your favorite scripting language

Solution

def PPV_OR(odd_ratio, power, alpha, verbose=True):
    """
    returns PPV from odd_ratio, power and alpha
    
    parameters:
    -----------
    odd_ratio: float
        P(H_A)/(1-P(H_A))
    power: float
        Power for this study
    alpha: float
        type I risk of error
        
    Returns:
    ----------
    float
        The positive predicted value
    
    """
    
    ppv = (power*odd_ratio)/(power*odd_ratio + alpha)
    if verbose:
        print("With odd ratio=%3.2f, "
               "Power=%3.2f, alpha=%3.2f, "
               "We have PPV=%3.2f" %(odd_ratio,power,alpha,ppv))
    return ppv

Second define a function to display easily the results

Solution

def plot_ppv(xvalues, yvalues, xlabel, ylabel, title):
   '''
   simply plot yvalues against xvalues, with labels and title
   
   Parameters:
   -----------
   xvalues, yvalues : iterables of numbers
   labels and title : string
   '''
   
   fig = plt.figure();
   axis = fig.add_subplot(1, 1, 1)
   axis.plot(xvalues, yvalues, color='red', marker='o', linestyle='dashed',
           linewidth=2, markersize=14);
   axis.set_xlabel(xlabel,fontsize=20);
   axis.set_ylabel(ylabel,fontsize=20);
   axis.set_title(figure_title, fontsize=20);
   return fig, axis

Last play with parameters : first, let's vary power

Solution

#-----------------------------------------------------------------
# An example
R = 1./5.
Pw = .5
alph = .05
ppv = PPV_OR(R, Pw, alph)

#-----------------------------------------------------------------
# Vary power:
Pw = np.arange(.1,1,.2)
ppvs = [PPV_OR(R, pw, alph, verbose = False) for pw in Pw]
xlabel = 'Power'
ylabel = 'PPV'
figure_title = 'With an odd ratio of {odd_ratio}'.format(odd_ratio=R)

#-----------------------------------------------------------------
# print
plot_ppv(Pw, ppvs, xlabel, ylabel, figure_title);

Then, let's vary odd ratio

Solution

#-----------------------------------------------------------------
# Vary odd ratio:
Pw = .5
alph = .05
odd_ratios = np.arange(.05,.5,.05)
ppvs = [PPV_OR(R, Pw, alph, verbose = False) for R in odd_ratios]

#-----------------------------------------------------------------
# print
figure_title = 'With a power of {power}'.format(power=Pw)
xlabel = 'odd_ratios'
ylabel = 'PPV'
plot_ppv(odd_ratios, ppvs, xlabel, ylabel, figure_title);

Last, let's vary alpha, remember that p-hacking may give us large type I risk of errors

Solution

#-----------------------------------------------------------------
# Vary alpha:
Pw = .5
R = 1/5
alphas = np.arange(0, .2, 0.01)# [0.001, .005, 0.01, 0.05, 0.1] #, 0.2, 0.3, 0.4, 0.5]
ppvs = [PPV_OR(R, Pw, alph, verbose = False) for alph in alphas]

#-----------------------------------------------------------------
# print
xlabel = 'alpha'
ylabel = 'PPV'
figure_title = 'With a power of {power} and odd ratio of {odd_ratio}'.format(
                                        power=Pw, odd_ratio=R)
plot_ppv(alphas, ppvs, xlabel, ylabel, figure_title);
#-----------------------------------------------------------------

This is also in a python notebook

The above discussed points can also be explored within this jupyter notebook

How to work with the notebooks ?

There are two cases.

You do not really know python, and how to install the jupyter notebook. You can still read the notebook, skipping the code sections. The notebook will introduce some definitions, and then play with different settings. But the true benefit comes if you can install the jupyter project see here and actually play with the code, for instance changing the sample size or effect size to understand better what power is.
Download the notebook, and try to understand the concepts and the code. If the code is unclear, please make an issue on the repronim github site.
Run it interactively on binder.

Key Points

A significant (say at the 0.05 level) may have a low chance of replication.

The PPV estimates the probability that the alternative hypothesis $H_A$ is true given that the test is significant at some $\alpha$ level.

This probability depends on several factors such as power $\beta$, $\alpha$ level, but also the prior chance that $H_A$ is true.